[기초수학] 함수

공부용으로 작성되는 페이지입니다. 틀린 부분이나 환경에 따라 오류가 발생할 수 있습니다. 

 

---

1. 함수의 기초 

1-1 함수의 정의 

함수 - 위키백과, 우리 모두의 백과사전

 

함수란 X라는 집합과 Y라는 집합이 있을 때, 두 집합의 대응관계를 의미한다.

X에서 Y로 대응되는 함수는 y =f(x)로 나타낸다.

 

함수는 다음 두 규칙이 성립되어야 한다.

1. 첫 번째 집합의 모든 원소에 대한 대응 관계가 존재  (= 첫 번째 집합의 모든 요소가 사용되어야 함)
2. 첫 번째 집합의 원소는 두 번째 집합의 한 원소에만 대응되어야 함 

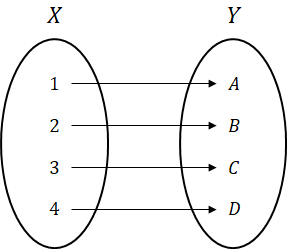
EX) 함수가 아닌 경우 

 

위 그림의 경우 집합 X의 원소 3,4는 집합 Y에 대응관계가 없으며(첫 번째 규칙 위반)

원소2가 집합 Y의 두 원소에 동시에 대응하고 있으므로 함수가 아니다.

 

 

1-2 함수 용어

• 정의역(Domain)
• 공역(Codomain)
• 치역(Range)

 

정의역은  함수가 어떤 값을 대응시키는지가 정의된 원소들로 구성된 집합으로, 쉽게 생각하자면 첫 번째 집합을 의미한다. 

공역은 정의역에 대응하는 영역이라는 의미로, 쉽게 생각하자면 두 번째 집합을 의미한다.

 

모든 원소가 대응되어야하는 정의역과 달리 공역은 그럴 필요가 없기 때문에 정의역에 대응되는 공역의 원소만 따로 부분집합을 형성할 수 있는데 이 영역은 치역이라고 한다.  

 

 

• 입력(Input) : 함수에 사용하는 정의역의 요소
• 출력(Output) : 입력에 대응하는 공역의 요소 

 

프로그래밍 관점에서 함수

 

1-3 함수의 종류

1. 전사함수 : 공역의 모든 요소가 정의역에 대응되는 함수 

   

   공역 = 치역

2. 단사함수 :  정의역과 공역의 요소가 일대일로 대응되는 함수 

   

   원소 C가 대응을 하지 않고 있으므로 전사함수는 아니다.

   
   
3. 전단사함수 : 정의역과 공역의 모든 요소가 빠짐없이 일대일로 대응되는 함수

   

4. ㅇ
5. ㅇ
6. ㅇ
7.  

 

2. 곱집합

2-1 곱집합의 정의

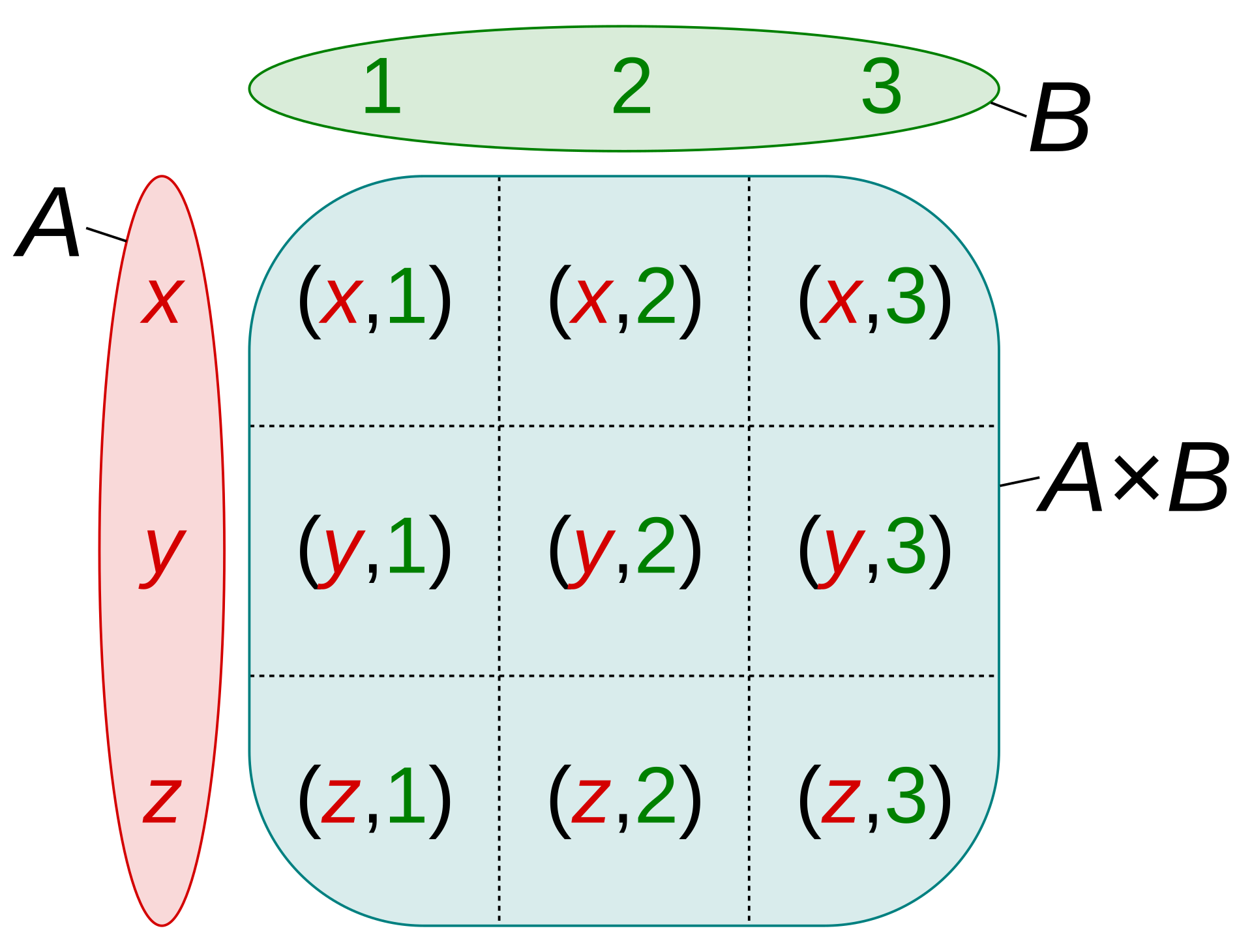
곱집합이란 두 집합의 원소를 순서쌍으로 묶은 원소의 집합을 의미한다.

 

ex) 

 

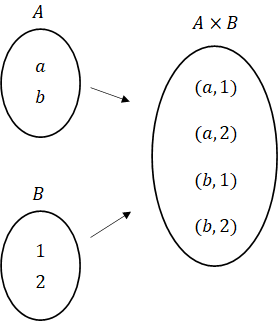
두 집합 A와 B의 각 집합에 속한 원소를 a, b 라고 했을 때 곱집합은? 

  = > AXB

 

곱집합의 원소는 각 집합의 원소를 순서쌍으로 묶어 튜플형식으로 표현한다.

=> (a,b)

 

곱집합을 통해 4개의 원소를 가지고 있는 집합 탄생

1번 이미지를 보고 보면 파악하기 쉽다

 

3. 합성함수

2개의 함수를 연쇄적으로 이어서 하나의 함수로 만드는 연산을 함수의 합성이라고 한다. 

 

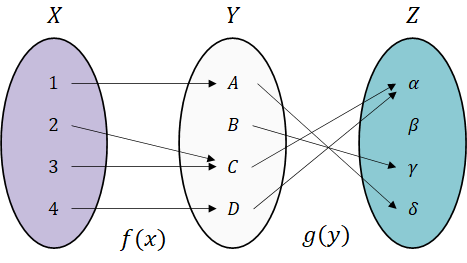
예를 들어 두 함수 f(x)와 g(y)를 연쇄적으로 합성함수로 만들면 

 

 

 

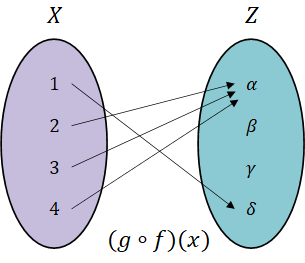
집합 y를 생략하고 표현할 수 있다. 

이러한 합성함수는 g o f 또는 g(f(x))로 표시한다. 먼저 실행되는 함수 f 가 기호(o)의 오른쪽에 놓이므로 주의할 것 

 

 

3-1 항등함수(identity function)

 

정의역과 공역이 동일한 값으로 대응되는 함수를 말한다.

기호로는 i라고 표현한다.

 

3-2 역함수(Inverse Function)

 

 

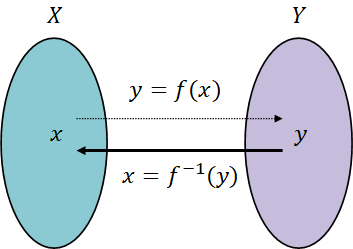
앞 시간에서 배웠던 역원과 같은 개념으로,

두 집합의 대응 관계를 뒤집어 공역Y에서 정의역 X로 대응하는 함수로도 생각할 수 있다. 

 

역함수에서 주의해야할 점은 모든 함수가 역함수를 갖지 않는다는 점이다.

역함수는 전단사 함수일 때만 역함수가 존재한다.

 

 

3-3 합성함수에 역함수 적용하기

g o f

 

 

g의 역함수를 먼저 실행하고 f의 역함수를 먼저 실행한다.

 

 

 

참고자료

 

함수 | 게임 엔진을 지탱하는 게임 수학

 

 

025. 전사 vs 단사 vs 전단사